GRE Quantitative Reasoning - GRE Practice Online

Select Exercise Lists

By Question Type
Quantitative comparison
Numeric Entry
Word Problem
Data Interpretation

By Content
Arithmetic
Algebra
Geometry
Data Analysis

Overview and Practice of GRE Quantitative Reasoning

1 Overview

GRE general test includes a math-related section: quantitative reasoning. It evaluates the ability to reason quantitatively and to address problems with quantitative methods, or say necessary mathematical skills.

The questions are in two sorts:

Pure mathematical problems: answer by math knowledge only
Word problems: answer by modeling problems mathematically

The mathematical symbols, terminology, and conventions in the Quantitative Reasoning worksheets are understandable at the high school level. Besides, there are some other assumptions listed in the Quantitative Reasoning section directions:

All numbers used are real numbers.
All figures are in a plane unless otherwise indicated.
Geometric figures are not necessarily drawn to scale.
Coordinate systems are drawn to scale

You can use a calculator in the test, but you cannot use your own calculator. In the computer-based GRE test, the calculator is provided on-screen; as for paper-delivered test, the test center will offer a basic calculator. You may get latest and official information of GRE Quantitative Reasoning from Quantitative Reasoning Measure.

2 GRE Quantitative Reasoning

GRE Quantitative Reasoning isn't real math test. It doesn't test all high school math skills; for example, it does not include trigonometry, calculus, or other higher-level mathematics. Instead, it just covers four primary math parts: arithmetic, algebra, geometry, and data analysis.

Arithmetic Topics include properties and types of integers, arithmetic operations, exponents and roots, and concepts of estimation, percent, absolute value, the number line, and decimal representation.

Example:

Directions: Compare Quantity A and Quantity B, using additional information centered above the two quantities if such information is given, and select one of the following four answer choices:

Quantity A is greater.
Quantity B is greater.
The two quantities are equal.
The relationship cannot be determined from the information given.

A symbol that appears more than once in a question has the same meaning throughout the question.


Ravi has more than twice the number of marbles that Sita and Tim have together.

Quantity A	Quantity B

The number of marbles that Ravi has	Three times the number that Sita and Tim have together.

	Quantity A is greater.
	Quantity B is greater.
	The two quantities are equal.
	The relationship cannot be determined without further information.

Exercises of arithmetic topics

Algebra Topics include operations with exponents; algebraic expressions; equations and inequalities; linear and quadratic equations and inequalities; and coordinate geometry, including graphs of functions, intercepts and slopes of lines.

Example:


y=x² + 1

Quantity A	Quantity B

xy	y³

	Quantity A is greater.
	Quantity B is greater.
	The two quantities are equal.
	The relationship cannot be determined without further information.

Exercises of algebra topics

Geometry Topics include parallel and perpendicular lines, circles, triangles, quadrilaterals, other polygons, three-dimensional figures, area, perimeter, volume, and angle measurement in degrees. (Not need to construct proofs of geometry.)

Example:


Point P has the coordinates (3,7) and point Q has the coordinates (-7,3) on the same rectangular coordinate plane.

Quantity A	Quantity B

Distance from the origin (0,0) to point P	Distance from the origin to point Q

	Quantity A is greater.
	Quantity B is greater.
	The two quantities are equal.
	The relationship cannot be determined without further information.

Exercises of geometry topics

Data Analysis Topics include basic descriptive statistics; interpretation of data in tables and graphs; elementary probability; conditional probability; random variables and probability distributions, including normal distributions; and counting methods, such as combinations and permutations.

Example:




Quantity A	Quantity B

The average (arithmetic mean) of 16, 23, and 52	The average (arithmetic mean) of 15, 24, and 51

	Quantity A is greater.
	Quantity B is greater.
	The two quantities are equal.
	The relationship cannot be determined without further information.

Exercises of data analysis topics

3 GRE Quantitative Reasoning Question Type

GRE Quantitative Reasoning has four common types of questions. A question may be promoted in two ways: either independently as a discrete question or as part of a set of questions, the latter case is usually in Data Interpretation whose all questions are based on the same data source, like tables or graphs.

Quantitative Comparison is the primary type in GRE quantitative reasoning and usually ask you select one answer choice from multiple options.

Exercises of quantitative comparison

Example:




Quantity A	Quantity B

40,000	(201.70)²

	Quantity A is greater.
	Quantity B is greater.
	The two quantities are equal.
	The relationship cannot be determined without further information.

Numeric Entry needs you calculate the answer; some Words Problem question also needs you give the numeric answer after modeling.

Exercises of numeric entry

Example:

Directions: Enter your answer as an integer or a decimal if there is a single answer box OR as a fraction if there are two separate boxes — one for the numerator and one for the denominator.

The sides of a rectangular piece of card are each 10 per cent too long for a particular project. By what percentage is the area too large?

Word Problem emphasizes to translate the problem to the mathematical model, you need to calculate the answer, select one or more choices from multiple options.

Exercises of word problem

Example:

Directions: Select answer choice or choices.

3x + y = 19 , and x + 3y = 1. Find the value of 2x + 2y

	20
	18
	11
	10
	5

Data Interpretation usually has a set of questions based on the same data source; the problems are diversity, like calculating the answer, selecting one or more choices from multiple options.

Exercises of data interpretation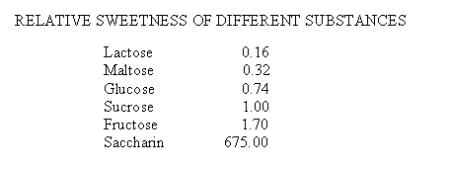

Example:

Directions: Questions 1 to 2 are based on the following data.

1. How many grams of sucrose (to the nearest gram) must be added to one gram of saccharin to make a mixture that will be 100 times as sweet as glucose?)

	1.
	8
	9
	10
	100

2. What is the ratio of glucose to lactose in a mixture as sweet as maltose?

	8 : 21
	21 : 8
	25 : 9
	29: 8
	32: 5